Sequential Logic & Sync
Combinational components within an electronic device require a certain amount of time \(t_{pd}\) to produce meaningful results. Over this time-frame we need to hold its input stable, however external input is unreliable, so theres no guarantee that this requirement is fulfilled. Additionally, we also want to make a sequential logic device that has the following structure:

For this purpose, we need to make some kind of device that is capable of "retaining" the value of a previously valid input.
D-Latch¶

If G is 1, then the value of D is passed to Q.
If G is 0, then the value of Q' is passed back to Q, and the value of D does not make a difference to the output.
This way, G acts as a "write-enable" and D is the input. A D-Latch can also be made by modifying an S-R NOR Latch with two AND gates and a write-enable input and setting \(R = S'\)
Storage of invalid information: If G changes from 1 to 0 at the exact moment when D just turned invalid from previously being valid, then we might end up storing that invalid value of D when the latch enters memory mode.
The Dynamic Discipline¶
To address the issue of storing invalid information:
The dynamic discipline states that there are two timing requirements for the input signal supplied at D, named as \(T_{setup}\) and \(T_{hold}\) which are:
- \(T_{setup} \approx 2 \times t_{pd}\) of the components that make up the D-latch.
- \(T_{hold} \approx t_{pd}\) of the components that make up the D-latch.
\(T_{setup}\) is defined as the minimum amount of time that the voltage on wire D needs to be valid/stable before the clock edge changes from 1 to 0 (turning from write mode to memory mode). This is the time you need to wait to ensure that the output at Q reflects what was supplied at D (\(1 \times t_{pd}\)) and to ensure that Q maintains this value (from the feedback) \(1 \times t_{pd}\) even after the input G has turned to 0.
\(T_{hold}\) is defined as the minimum amount of time that the voltage on wire D needs to be valid/stable after the clock edge reaches a valid 0 from a previous 1. This is the time required for the D-Latch to realise that it has switched from write to memory mode (\(1 \times t_{pd}\))
Edge-Triggered D Flip-Flop¶
Notice that if we want to use a D-Latch register in a sequential logic device of the form shown above, there is a problem. When the D-Latch feeds its new state into the sequential logic device, it gets back an output containing the next state of the device. If the latch is still in write mode at this time, we will fall into an infinite loop cycle which keeps updating the state of the sequential logic device even though we only intended to move it forward just once! Making a clock that is perfectly timed so that this doesn't happen is tedious, and it is thus better to have a system such that the next state waits to enter the latch until the next clock cycle. If we could somehow make it so that the latch was only in write mode at the rising (or falling) edge of the clock pulse, we would have what we want!

The output of the D-Flip-Flop shown above does exactly this. It follows the value of D only at rising edges of the clock.
Why is this the case? The master latch is "transparent" to the D input as long as the clock is low, but when the clock goes high, the last value for D that was fed into the master latch while G was low is what the output of the master latch (*) now becomes. Now that G is high, this value of D that was recorded is now propagated through the slave latch, and we finally get its output at Q! When the clock goes low, the slave latch enters memory mode. Even if the * value changes now (= D) it won't affect Q! Thus, we have a rising edge triggered D Flip Flop!
Following the same logic, we can make it such that the flip flop is triggered by falling edges instead by putting the inverter on the slave latch.
There is one last problem to address. When the clock goes low, if the output of the master latch (*) changes before the slave latch realises that it has entered memory mode, Q will become invalid. Thus, To ensure proper operation, the \(t_{cd}\) of the master latch must be larger than the \(t_{hold}\) of the slave latch.
\(t_{cd}\) and \(t_{pd}\)¶
\(t_{cd}\) of an SLD is the time that it takes for the output of the SLD to change (be invalid) after the rising clock pulse
\(t_{pd}\) of an SLD is the time that it takes for the output of the SLD to become stable after the rising clock pulse (after this amount of time has passed after the rising clock pulse, the output is guaranteed to not change)
The SLD Timing Constraint¶
Consider the following circuit:
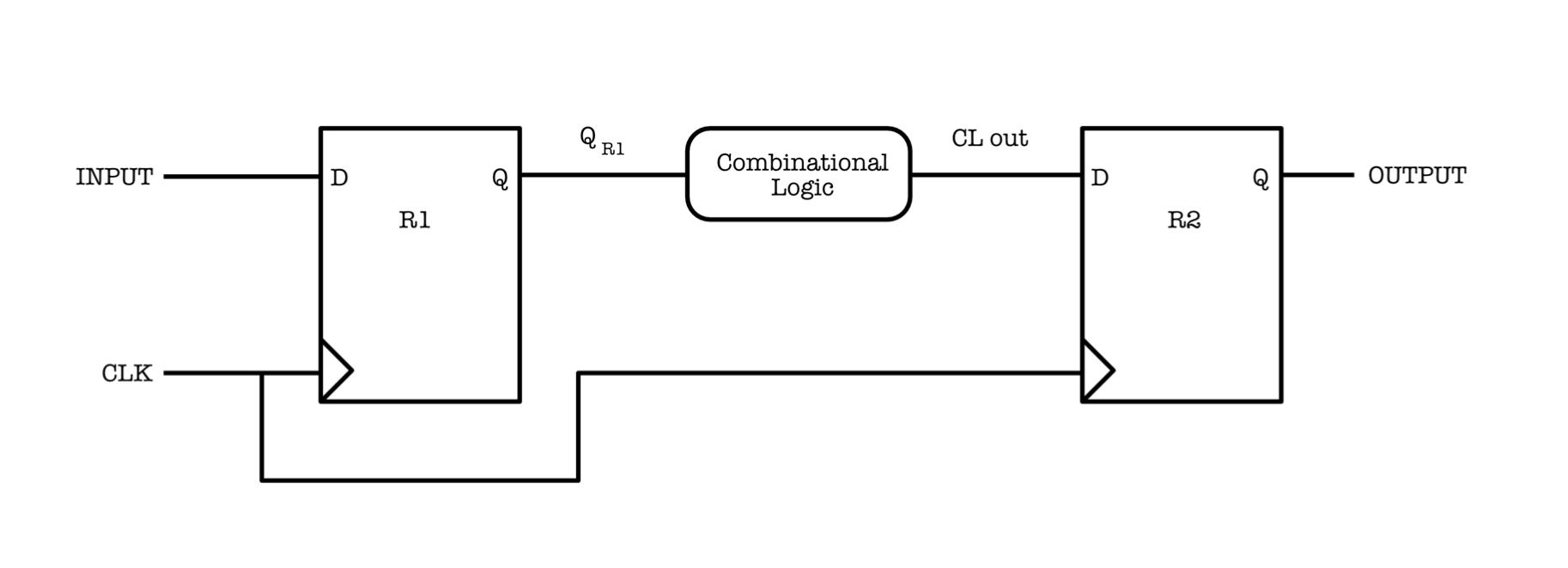
If the input to register 2 changes before its hold time (after a rising clock pulse) then the dynamic discipline is violated.
\(t_1 = t_{cd, R_1} + t_{cd, L} > t_{hold, R_2}\) Here, \(t_1\) is the minimum time taken for the input at register 2 to change after a rising clock pulse.
Before a new rising clock pulse, \(R_1\) & \(L\) must have produced a valid output. Additionally, we also want to allow for the setup time of \(R_2\) to pass after said valid output has been produced to ensure that \(R_2\) holds on to this output. Thus,
\(t_2 = t_{pd, R_1} + t_{pd, L} + t_{setup, R_2} < t_{clk}\)
Metastable State¶
This single synchronous clock discipline ensures that all of our components of the circuit are working properly. However, there is one last problem. In practice, the external input D cannot be made to obey the dynamic discipline of the first DFF every single time. If the dynamic discipline is violated, it is possible that the device is fed with an invalid voltage input, and it will thus produce an invalid voltage ouput.

Looking at the D-Latch's VTC, we realise that if the \(V_{in}\) is far away from the point where \(V_{in} = V_{out}\), then it will automatically stray towards either a 0 or a 1. However, if \(V_{in} = V_{m}\) (or sufficiently close to it) then it will take forever for the voltage to come back to being a proper 0 or a 1.
The state where our SLD is unable to settle to a stable value for unknown period of time is called the metastable state. Obviously we do not want this because the output of the device is invalid during this unknown time frame.